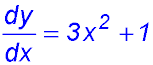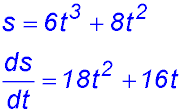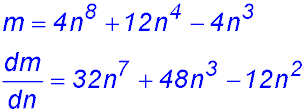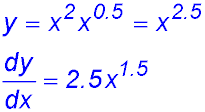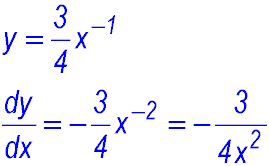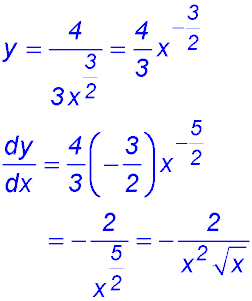Dr. J's Maths.com
Where the techniques of Maths
are explained in simple terms.

Calculus - Differentiation - Basic techniques.
Test Yourself 1 - Solutions.


 

Differentiate each of the following functions with respect to the given variable. All questions use only the direct technique as described - no special rules.

As always - your first step is to look at the structure and decide what you need to do.

Find the gradient function of the following functions - that is "differentiate each of the following functions":
1. Basic format. 1. y = x3 + x

2. y = 3x3 + 2x2 - x - 42

y' = 9x2 +4x - 1

 3. y = 4x2 + 5x

y' = 8x + 5
  4. y = 3t - 5t2

y' = 3 - 10t

 5. y = 0.5x4 + 1.5x2 - 42

y' = 2x3 + 3x

 6. y = x2.5

y' = 2.5 x1.5
2. Simple brackets. 7. s = 2t2(3t + 4)

8. m = 4n3(n5 + 3n - 1)


9. y = 3x3(2x4 - 5x2 - x)

y = 6x7 - 15x5 - 3x4

y' = 42x6 - 75x4 - 12x3
3. Use of d/dx. 10.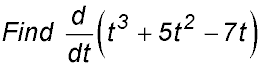

= 3t2 + 10t - 7

 11.

= 3u2 + 10u - 12

 12.

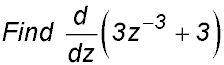
= -9z-4
  13.

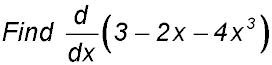
Derivative = -2 - 12x2

 14.

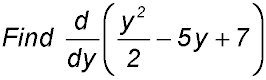
Derivative = y - 5

 15.

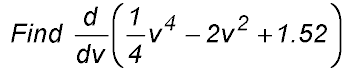
Derivative = v3 - 4v
4. Radicals. 16.

17.

18.

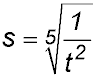
  19. 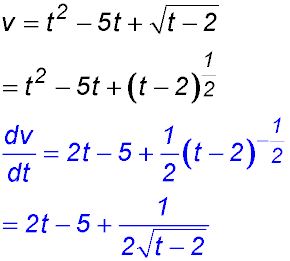20.

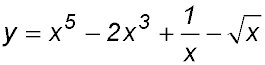
21.

5.Use of negative signs. 22.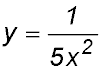

23.

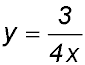
24.

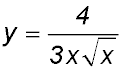
  25.

 

 26. 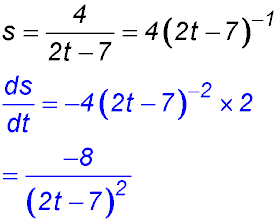27.
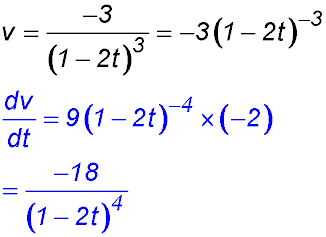6. Fractions with 1 term in the denominator. 28.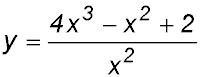

y = 4x - 1 + 2x-2

y' = 4 - 4x-3

 

 29.

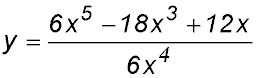
= x -3x-1 + 2x-3

y' = 1 + 3x-2 - 6x -4

 30.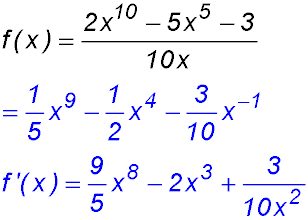